Number Systems

The number system is a way to represent or express numbers. You have heard of various types of number systems such as the whole numbers and the real numbers. But in the context of computers, we define other types of number systems. They are:

1. Binary Number System
2. Octal Number System
3. Decimal Number System
4. Hexa-Decimal Number System

• 1. Binary Number System

A computer can understand only the ON and OFF state of a switch. These two states are represented by 1 and 0. The combination of 1 and 0 form binary numbers. The binary number system uses Base 2. Each digit in a binary number is called a bit. So, a binary number 1001 has 4 bits.

Examples: (1001)₂; (1010)₂; (1111)₂

• 2. Octal Number System

This system uses digits 0 to 7 (i.e. 8 digits) to represent a number and the numbers are as a base of 8.

Examples: (24)₈, (205)₈

• 3. Decimal Number System

In this number system, the digits 0 to 9 (i.e. 10 digits) represents numbers. As it uses 10 digits to represent a number, it is also called the base 10 number system. Each digit has a value based on its position called place value. The value of the position increases by 10 times as we move from right to left in the number.

For example, the value of (125)₁₀ is

= 1 x 10² + 2 x 10¹ + 5 x 10⁰

= 100 + 20 + 5

• 4. Hexa-Decimal Number System

In this system, the digits 0 to 9 and A to F (i.e. 16 digits) represent numbers. Thus it is also known as the base 16 number system. Each digit position represents a power of 16. As the base is greater than 10, the number system is supplemented by letters. Following are the hexadecimal symbols: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E, and F. All the other numbers can be expressed with the help of combination of these digits and alphabets. A, B, C, D, E, F represents 10, 11, 12, 13, 14 & 15 respectively.

Units of measurement of data:

Machine language is binary. And so it is necessary to discuss how to measure the data stored in a computer. Bit and Byte are the units to measure data.

• Bit

It is the smallest unit of memory or instruction that can be given or stored on a computer. A bit is either a 0 or a 1.

• Byte

A group of 8 bits like 00001111 is a byte. Combination of bytes comes with various names like the kilobyte. One kilobyte is a collection of 1000 bytes in decimal and 1024 bytes in binary. 1024 kilobytes form a Megabyte (Mb) and so on.

In the binary number system, units of information are expressed as multiples of bits. For example-

UNIT	ABBREVIATION	STORAGE
Bit	B	Binary Digit, Single 1 or 0
Nibble	-	4 bits
Byte	B	1 Byte = 8 bits
Kilobyte	KB	1 Kilobyte = 1024 bytes
Megabyte	MB	1 Megabyte = 1024 KB
Gigabyte	GB	1 Gigabyte = 1024 MB
Terabyte	TB	1 Terabyte = 1024 GB
Petabyte	PB	1 Petabyte = 1024 TB
Exabyte	EB	1 Exabyte = 1024 PB
Zettabyte	ZB	1 Zettabyte = 1024 EB
Yottabyte	YB	1 Yottabyte = 1024 ZB

Converting Decimal Numbers to Binary Numbers:

Integer Part:

• Step 1: Divide the decimal number by 2 repeatedly.
• Step 2: Keep a note of the remainder on the right-hand side, it should be between 0 and 1.
• Step 3: Repeat the steps until the quotient is equal to 0.
• Step 4: Write out all the remainders, from bottom to top.

Fraction Part:

• Step 1: To convert fraction to binary, start with the fraction in question and multiply it by 2.
• Step 2: Keeping notice of the resulting integer and fractional part.
• Step 3: Continue multiplying by 2 until you get a resulting fractional part equal to zero.
• Step 4: Then just write out the integer parts from the results of each multiplication.

Let us consider a few examples-

Example 1: Converting decimal number 25 into its binary equivalents.

Thus, the decimal number 25 is equal to 1 1 0 0 1 in binary form.

Therefore it can be expressed as ( 25 ) ₁₀  =  ( 1 1 0 0 1 ) ₂. The base of the number is written as subscript.

Example 2: Converting decimal number 29 into its binary equivalents.

Thus, the decimal number 29 is equal to 1 1 1 0 1 in binary form.

Therefore it can be expressed as ( 29 ) ₁₀  =  ( 1 1 1 0 1 ) ₂. The base of the number is written as subscript.

Example 3: Converting decimal number 29 into its binary equivalents.

Thus, the decimal number 125 is equal to 1 1 1 1 1 0 1 in binary form.

Therefore it can be expressed as ( 125 ) ₁₀  =  ( 1 1 1 1 1 0 1 ) ₂. The base of the number is written as subscript.

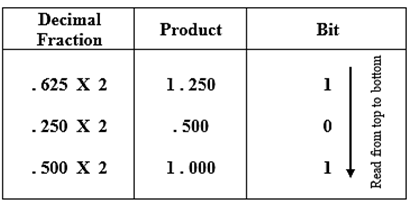
Example 4: Converting decimal fraction number 0.625 into its binary equivalents.

Thus, the decimal fraction number 0.625 is equal to 0 . 1 0 1 in binary form.

Therefore it can be expressed as (0.625) ₁₀ = ( 0 . 1 0 1 ) ₂. The base of the number is written as subscript.

Example 5: Converting decimal number 37.25 into its binary equivalents.                                                                                  

Thus, the decimal fraction number 37.25 is equal to 1 0 0 1 0 1 . 0 1 in binary form.

Therefore it can be expressed as (37.25) ₁₀ = ( 1 0 0 1 0 1 . 0 1 ) ₂. The base of the number is written as subscript.

Share This